Method Development
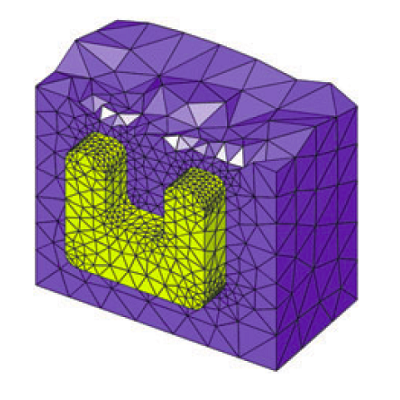
Fig.1: Tetrahedral mesh defining a split ring resonator for use in numerical calculations. Figure adapted from Laser & Photonics Reviews 5, 773 (2011).
A significant part of theoretical physics is concerned with developing and refining analytical and numerical methods for the investigation of specific classes of physical problems and systems. The group has been - and continues to be - actively contributing to the development of purely numerical calculation methods such as
- The Discontinuous-Galerkin Time-Domain Method for the Maxwell Equations
- Rigorous Coupled Wave Analysis (a.k.a. Fourier Modal Method) for Periodic Systems
- The Multi-Scale Methods for Periodic Systems
- The Photonic Wannier Function Method
- Photonic Band-Structure Computations
as well as partly or purely analytical approaches such as
- Quasinormal mode theory for optical cavities and plasmonic nano resonators
- Quantum-Field-Theoretical approaches for photon transport problems
- Strain Computations
Certain aspects of these methods are also of considerable interest to applied mathematicians and we enjoy a particularly fruitful collaboration with the Collaborative Research Center (CRC) 1173 Wave Phenomena: Mathematics and Numerics.
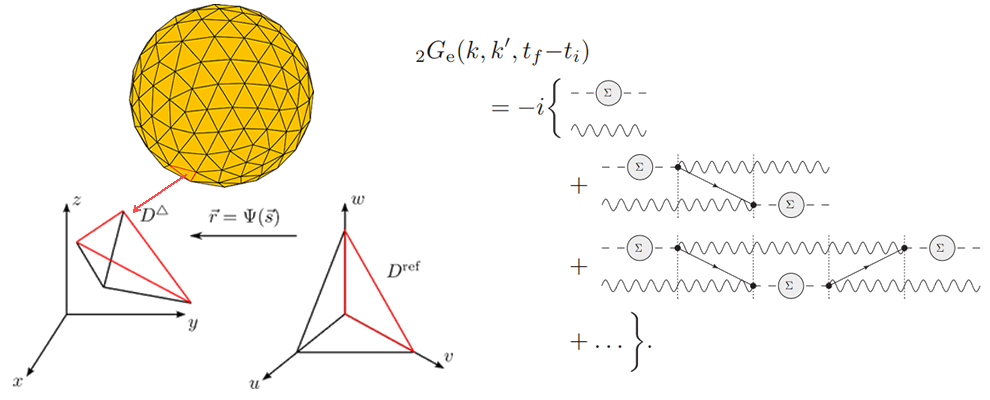
Fig.2: Left: Details of the construction of efficient time-domain finite element solvers for the Maxwell equations. Right: Quantum-field theoretical approach based on Feyman diagrams for the investigation of few-photon transport problems in waveguiding structures with embedded quantum emitters (adapted from Physical Review A 93, 013828 (2016)).



